Type inhabitation

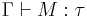In type theory, a branch of mathematical logic, in a given typed calculus, the type inhabitation problem for this calculus is the following problem^[1]: given a type $\tau$ and a type environment $\Gamma$ , does there exist a $\lambda$ -term M such that $\Gamma \vdash M�: \tau$ ? With an empty type environment, such an M is said to be an inhabitant of $\tau$ .

Contents

1 Relationship to logic
2 Formal properties
3 See also
4 References

Relationship to logic

In the case of simply typed lambda calculus, a type has an inhabitant if and only if its corresponding proposition is a tautology of minimal implicative logic. Similarly, a System F type has an inhabitant if and only if its corresponding proposition is a tautology of second-order logic.

Formal properties

For most typed calculus, the type inhabitation problem is very hard. Richard Statman proved that for simply typed lambda calculus the type inhabitation problem is PSPACE-complete. For other calculi, like System F, the problem is even undecidable.

See also

Curry–Howard isomorphism

References

^ Pawet Urzyczyn (1997). "Inhabitation in Typed Lambda-Calculi (A Syntactic Approach)". Lecture Notes in Computer Science (Springer): 373–389. http://www.springerlink.com/index/tg515q64xn434l70.pdf.